技術コラム【吐出の羅針学】吐出における粘性の影響

べき乗則流体とは

べき乗則流体とは、非ニュートン流体のうち、擬塑性流体、ダイラタント流体のように、みかけ粘度η[Pa･s]とずり速度D[s-1]の関係が、

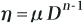
または、せん断力τとずり速度Dの関係が、

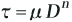
で表されるような流体を指します。

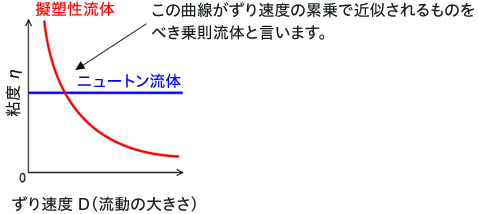
つまり、ずり速度の増減により、みかけ粘度が累乗的に増減するような流体を『べき乗則流体』といいます。ここでμは粘性係数と呼ばれますが、ニュートン流体では粘度と一致します。また n は粘性指数と呼ばれます。

ニュートン流体は上式で n=1 のときの特別解で、n>1 ならばダイラタント流体、n<1 ならば擬塑性流体となります。すなわち、『べき乗則流体』とは、ニュートン流体、擬塑性流体、ダイラタント流体の3つの流体の総称ということです。

非ニュートン流体では、ずり速度Dにより粘度は変化するため、ニュートン流体のように一定の値の粘度がありません。したがって『あるずり速度での粘度』＝みかけの粘度でしか粘性を表現できないため、ηをみかけ粘度と呼びます。

粘度と円管摩擦圧力損失の関係

圧力損失は、配管などの耐圧設計や供給装置の能力を決める上で極めて重要です。べき乗則流体の場合の円管摩擦圧力損失ΔP[Pa]は、ニュートン流体と同様に次式で表されます。

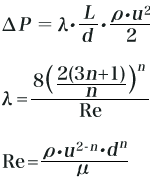
※d：管径[m]、L：管長[m]、u：平均流速[m/s] 、ρ：密度[kg/m³]、λ：管摩擦係数[無次元]、Re：レイノルズ数[無次元]、μ：粘性係数[Pa･s]、n：粘性指数[無次元]

粘度と流速の関係

流速分布は、特に塗布を行う上で重要です。べき乗則流体の場合、円管内の流速分布 u（r）は、管中心から r をとると、次式で表されます。

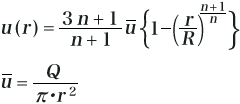
ここで、Rは管半径[mm]、Q[m3/s]は体積流量を示します。 ニュートン流体と同じで、べき乗則流体でも管壁の影響により、管壁（r＝R）では流速 u（R）＝0となります。上式より、管内の流速分布は粘性指数nの影響を大きく受けることがわかります。ある内径の管に、粘性指数nの違う流体を、同じ体積流量を流した場合、流速分布はそれぞれ次のようになります。

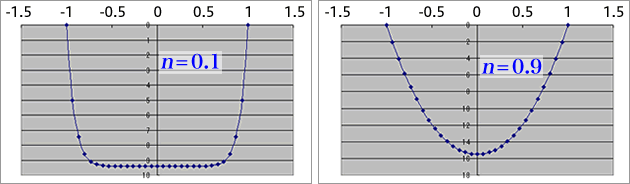
このグラフからわかるように、粘性指数が0に近づくほど栓流（プラグ流）、1に近づくほど放物線分布になるのがわかります。

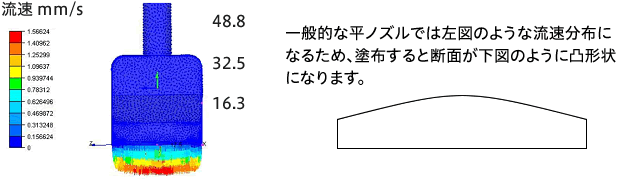
塗布の場合、吐出口でもこの流速分布となっているため、n＝0.1の流体で塗布すると平たくなり、n＝0.9の流体で塗布すると中央が盛り上がった形状に塗布されることになります。吐出口が円形ではなく方形の場合も円管と同様で、管壁での流速は0となることと、その流速分布は粘性指数に影響されるため、両端の流速が遅く中央ほど速くなり、塗布すると中央が盛り上がった形状になります。このため、均一膜厚での塗布を行うには、流路形状の工夫が必要となります。

チクソトロピーの影響

べき乗則流体のうち擬塑性流体では、ずりを受けると粘性が低下し、ずりを除去してもすぐに粘性が戻らないものがあります。この性質をチクソトロピーと言います。

チクソトロピーは、高分子系の流体で考えると理解しやすいです。高分子系の流体にずりをかけると、高分子鎖がのび、からまっていた高分子鎖がほどけるため抵抗＝粘性が低下します（擬塑性）。さらにずりを大きくすると、この高分子鎖が各所で切断（構造破壊）されるため、さらに粘性が低下します。一度、切断された高分子鎖はなかなか元に戻らないので、ずりを除去しても粘性はしばらく低下したままです。これがチクソトロピーです。

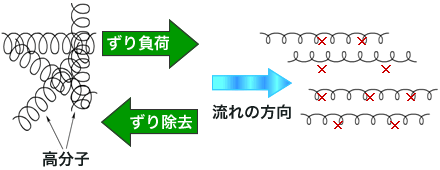
上図において、高分子鎖の切断（×印）が生じない場合は、ずりを除去すると元の状態に戻りますが（擬塑性）、高分子鎖の切断が生じた場合は元の状態に戻るには時間がかかります。つまり、見た目の粘性が低下します。

流速が速かったり、管径が極めて細い場合、ずりが大きくなるため、流体の構造は破壊されます。このため、吐出前後で液の性質が変化する場合がありますので、チクソトロピー性の高い流体においては、注意が必要です。