技術コラム【吐出の羅針学】等量分岐

前回は、等量分岐を行うにあたって必要な「主な管路抵抗と計算式」について説明しました。なかなかややこしいかもしれませんが、管路設計の基本となりますので、時間のあるときにぜひ復習しておいてください。今回はいよいよ、等量分岐について説明します。

［分岐流量の求め方］

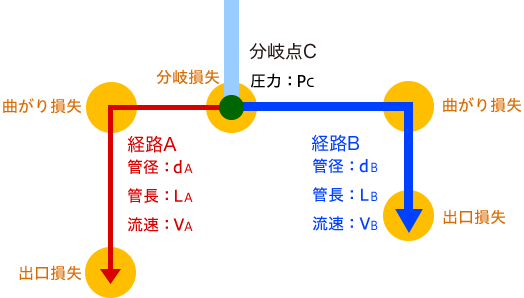
まずは前回の内容を踏まえて、図のような分岐管の流量を求めてみましょう。点Cにて経路A、経路Bに分かれる2分岐管で、それぞれは円管とします。分岐点Cの圧力をP_Cとすると、このP_Cは経路A、Bによらず、一意に定まります。このとき、点Cの圧力と大気圧との圧力差（ P_C－P₀ ）により、経路A、Bには流体が流れることになりますが、その流速（流量）は各経路の管路抵抗によります。では、さっそく管路抵抗を計算してみます。

前提条件

流体は、ニュートン流体かつ層流。
分岐損失は無視。
点Cには分岐損失が生じますが、前回説明したとおり、分岐損失は分岐角度や分岐部の形状、流量比、直径比、Re数などに依存するため、実験的に求めることが不可欠になります。よって、今回は無視することとします。
出口損失は無視。
大気への流出であるため、損失は極めて小さいとして無視します。

よって、経路A，Bでのそれぞれの総損失は、

【経路Aの損失ΔP_A】

【経路Bの損失ΔP_B】

となります。
冒頭で述べたように、点Cの圧力は経路A、Bによらず同じ値になるため、上式は等しく、

となります。
また、分岐前の流量をQとすると、

となります。
(a)、(b) 式を連立させると、V_A、V_Bを求めることができ、（b）の式に値を代入して流量を求めます。

［等量分岐をする場合］

等量分岐をしたい場合は、経路A、Bの流量が等しくなるため、

とし、(a)式と連立させて、d_A、L_A、d_B、L_Bの関係を求めます。

しかし、ほとんどの場合は計算が複雑になってしまうため、等量分岐を行う場合は、
・d_A＝d_B
・L_A＝L_B
とし、両経路の径、長さ、曲がりなどの各損失が同じになるよう、管路を対称設計とすることが一般的な考え方です。
（そうすることで、自動的に(a)、(c)式が成立します。）

キャプテンメッセージ

等量分岐は一見そんなに難しくなさそうですが、実際にやってみるとそう簡単ではありません。管路抵抗だけでもややこしいのに、さらに非ニュートン流体の場合は流体の粘度特性まで関係してきますので、等量分岐は非常に難しいです。
先日も、「完璧」に設計した…と思っていたのに、等量分岐できなかったことがありました。原因は流体に大きなチクソトロピー性があり分岐損失を読み違えたためでしたが、こういった分岐損失データは、世の中にまず、ありません。

どうしても分岐が必要な場合は、少なくとも一度は修正するつもりで、トライアル＆エラーで臨まれることをお勧めします。